import numpy as np
from matplotlib import pyplot as plt
import math
from IPython.display import Image
from numpy.polynomial.polynomial import Polynomial
from numpy.polynomial import Polynomial as P
from numpy.polynomial import Chebyshev
import ephem

Calcul des éphémérides par interpolation des polynomes de Tchebychev

Le calcul des éphémérides est depuis longtemps assuré par des méthodes puissantes et dont l'erreur est assez faible. Un premier pas dans ce large domaine est d'essayer d'interpoler la trajectoire de certains astres grâce aux polynômes de Tchebychev de première espèce. Cette famille de polynômes est notamment découverte par tous les élèves de classe préparatoire scientifiques. On s'intérésse donc à une application concrète de ce que l'on découvre en classe.

Dans le cadre des éphémérides, l'approximation lagrangienne (plus classique dans le cas général) par des polynômes consiste à faire passer, pour un intervalle donné, un polynôme de degré n par n+1 valeurs, alors qu'il serait préférable de tenir compte de toutes les valeurs de la fonction sur cet intervalle. L'approximation de Tchebychev s'impose pour cela, car elle est celle de plus bas degré dont l'erreur ne dépasse pas une valeur donnée a priori, et son erreur est régulièrement distribuée sur l'intervalle considéré.

Revue rapide des polynômes de Tchebychev

On peut définir les polynômes de Tchebychev de première espèce par : $$T_n(x)= \cos (n \arccos(x))$$ On montre par la suite les propriétés suivantes :

• i : Les polynômes de Tchebychev sont uniques
• ii : Ils vérifient la relation de récurrence : $\forall n \ge 2, \forall X \in [-1,1], T_{n+2}(X)=2X T_{n+1}-T_n (X)$
• iii : $\forall n \ge 2, deg(T_n)=n$ et il est de coefficient dominant $2^{n-1}$
• iv : On définit $\forall k \ \{0,... n-1 \}, \theta_k= \frac {(2k+1)\pi} {2n}$ de sorte que $( \cos(\theta_k))_k$ forme la famille des n racines distinctes du polynome $T_n$

De plus, l'intetêt vis à vis de ces polynômes vient du faite qu'ils forment une famille orthogonale de $ \mathbb R [X]$ pour le produit scalaire suivant : $$\forall P,Q \in \mathbb R [X], \langle P,Q \rangle = \int_{-1}^1 \frac {P(t) Q(t)}{\sqrt{1-t^2}} dt $$

En pratique, disposer d'une famille orthogonal est la clée pour exprimer un vecteur. S'il on dispose d'un vecteur (ici un polynome), on peut l'exprimer comme une combinaison linéaire des vecteurs de la base orthogonale (ici les $T_n$).

Définition de l'interpolation

Grossièrement, interpoler c'est trouver la trajectoire la plus cohérente en disposant d'une certains nombre de points. Pour mieux comprendre, intéréssons nous à une interpolation simple par les polynômes de Lagrange

Nous disposons des points suivants :

# Liste de points (x, y)
points = [(0, 1), (1, 3), (2, 2), (3, 5), (4, 4)]

# Séparer les points en deux listes : x et y
x_points, y_points = zip(*points)

# Afficher les points dans un plot
plt.scatter(x_points, y_points, color='red')
plt.plot(x_points, y_points, linestyle='dashed', color='blue')
plt.title('Points pour l\'interpolation de Lagrange')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.show()

On peut ensuite en faire l'interpolation, pour un degré $10$, cela donne :

# Fonction pour calculer l'interpolation de Lagrange
def lagrange_interpolation(x_points, y_points):
    poly = P([0.0])
    n = len(x_points)
    for i in range(n):
        p = P([1.0])
        for j in range(n):
            if i != j:
                p *= P([-x_points[j], 1.0]) / (x_points[i] - x_points[j])
        poly += p * y_points[i]
    return poly

# Calculer le polynôme d'interpolation
lagrange_poly = lagrange_interpolation(x_points, y_points)

# Afficher le polynôme d'interpolation
x_new = np.linspace(min(x_points), max(x_points), 100)
y_new = lagrange_poly(x_new)

plt.scatter(x_points, y_points, color='red', label='Points originaux')
plt.plot(x_new, y_new, label='Interpolation de Lagrange')
plt.title('Interpolation de Lagrange')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
plt.grid(True)
plt.show()

Revue des éphémérides

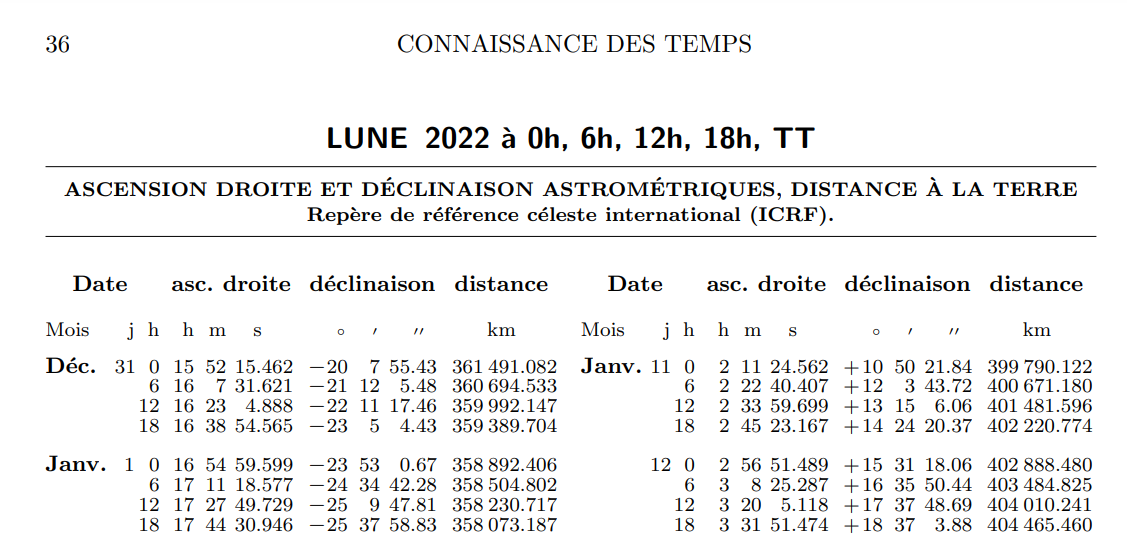
Les éphémérides sont des tables qui regroupent les positions d'astres pour des dates données. La revue la plus connue regroupant ces tables est la Connaissance des Temps. La Connaissance des Temps est une publication annuelle. Elle s'occupre de répertorier les éphémérides et autres données dans des tables succintes et pratiques pour la Terre, le Soleil, la Lune, et les autres planètes du système solaire. Trouvez ci-dessous un extrait des tables :

Image(url="ConnaissanceDesTemps.png", width=490, height=300)

Objectif

Considérons l'intervalle de temps $[t_0, t_0+DT]$ et $t \in [t_0, t_0+DT]$, on exprime la position (i.e la fonction $y(t)$) grâce aux polynômes de Tchebychev tel que : $$y= \sum_{k=0}^n a_kT_k(x)$$

où :

• $a_k$ désigne le k-ième coefficient de l'interpolation
• $T_k$ désigne le k-ième polynôme de Tchebychev
• $x$ est un paramètre que l'on calcul par $x=\frac {2(t-t_0)}{DT}-1$

remarque:

• on voit clairement par l'expression donnée que le paramètre $x$ appartient bien à l'intervalle $[-1,1]$ ce qui assure l'existence des polynômes en $x$.
• la validité de l'interpolation est restreinte à l'intervalle d'étude

Le but de notre démarche est de calculer ces coefficients afin de déterminer la trajectoire d'astres.

Mise en place de l'interpolation de la Lune

Mise en place des données

En pratique, on utilise une bibliothèque python permettant directement d'obtenir les données.

# Créer un observateur (par exemple, à Paris)
observer = ephem.Observer()
observer.lat = '48.8566'  # Latitude de Paris
observer.lon = '2.3522'   # Longitude de Paris
observer.elevation = 35   # Altitude en mètres

# Définir la plage de dates
dates = np.arange('2023-01-01', '2023-01-31', dtype='datetime64[D]')

#On crée un tableau d'indices pour identifier les dates à une valeur normalisée
indices_dates = np.arange(len(dates))
#on normalise les indices entre -1 et 1 :
indices_dates = 2 * (indices_dates - indices_dates.min()) / (indices_dates.max() - indices_dates.min()) - 1

# Stocker les résultats
ra_list = []
dec_list = []

for date in dates:
    observer.date = date.astype(str)  # Convertir en chaîne de caractères
    moon = ephem.Moon(observer)
    ra_list.append(np.degrees(moon.ra))  # Convertir en degrés
    dec_list.append(np.degrees(moon.dec))  # Convertir en degrés

On remarquera que indices_dates est bien une liste de valeurs normalisées dans l'intervalle $[-1,1]$

Interpolation

On se passe ici des calculs fastidieux des coefficients $a_k$, puique des bibliothques intégrées nous permettent de la calculer facilement.

poly_ra = Chebyshev.fit(indices_dates, ra_list, deg=len(indices_dates)-1)
poly_dec = Chebyshev.fit(indices_dates, dec_list, deg=len(indices_dates)-1)

Mais qu'est ce que l'ascension droite et la déclinaison ?
C'est un système d'axes adpaté au mouvement de rotation de la Terre (ce qui entraine celui des étoiles dans notre ciel).
Pour mieux comprendre, voir l'image suivante :

Image(url="RA.svg", width=490, height=300)

#affichage des résultats
t_plot = np.linspace(-1, 1, 100)
ra_plot = poly_ra(t_plot)
dec_plot = poly_dec(t_plot)

plt.figure(figsize=(12, 6))

# Ascension droite
plt.subplot(2, 1, 1)
plt.plot(indices_dates, ra_list, 'ro', label='Données ascension droite')
plt.plot(t_plot, ra_plot, 'b-', label='Interpolation ascension droite')
plt.legend()
plt.title("Ascension droite")
plt.xlabel("Temps normalisé")
plt.ylabel("RA (degrés)")

# Déclinaison
plt.subplot(2, 1, 2)
plt.plot(indices_dates, dec_list, 'go', label='Données Declinaison')
plt.plot(t_plot, dec_plot, 'm-', label='Interpolation Declinaison')
plt.legend()
plt.title("Déclinaison")
plt.xlabel("Temps normalisé")
plt.ylabel("Dec (degrés)")

plt.tight_layout()
plt.show()

Conclusion

On a donc réussit à déterminer une trajectoire cohérente pour la Lune grâce aux polynômes de Tchebychev : à n'importe quelle date de l'intervalle, nous pouvons avoir une idée très précise de la position de la Lune. Cependant, il faut garder en tête qu'il y a une part d'erreur liée à l'interpolation.